Visita el link:
http://www.educaplus.org/luz/lente1.html
Lee la informacion sobre Las lentes, y al final encontrarás un applet, con el cual podrás interactuar interactivamente con los tipos de lentes: divergentes y convergentes.
Mañana aclaramos las dudas que se den.
Un saludo, Hader V.
martes, 3 de agosto de 2010
jueves, 21 de enero de 2010
Estadística Grado 12º
INTRODUCCIÓN A LA ESTADÍSTICA
UN POCO DE HISTORIA
El uso de herramientas cuantitativas para el tratamiento de datos, tiene origen en épocas remotas. Se tiene información de hace más 3000 años antes de Cristo, donde las antiguas civilizaciones, como la Egipcia, aplicaron continuamente censos que ayudaban a la organización del estado y la construcción de las pirámides.
El antiguo testamento nos sugiere que Moisés ordenó un “Censo” a la población Israelita para identificar los miembros de las familias. En la antigua Grecia y el Imperio Romano, era común la aplicación de censos para la planificación de impuestos y la prestación del servicio militar.
La palabra estadística deriva del latín moderno statisticum collegium (“consejo de
estado”), del latín antiguo status (“posición”, “forma de gobierno”), de la palabra
italiana moderna statista (“estadista”, “político”) y del italiano antiguo stato (“estado”). En 1749, el alemán, Gottfried Achenwall (1719-1792) usa el término Statistik en su libro titulado “Staatswissenschaft der vornehmen Europäischen Reiche und Republiken”, quien originalmente designó la palabra estadística para el
análisis de los datos de un gobierno, definiéndola como la “Ciencia del Estado”. A
Gottfried Achenwall se le conoce como el “Padre de la Estadística”.
La primera persona que introdujo el término estadística en Inglaterra fue Sir John
Sinclair (1754-1835) con su trabajo “Statistical Account of Scotland” (1791-,1799) trabajo compilado en 21 volumenes. El autor explica en su libro, que la palabra estadística la adoptó gracias al estudio de investigaciones realizadas en Alemania, como una palabra novedosa que llamaría la atención de los ingleses; a diferencia, de que en Alemania la estadística se usa como instrumento para medir la fortaleza de un estado, mientras que Sinclair, la emplearía como generadora de información interna para encontrar falencias y proponer mejoras en el país. A este trabajo le siguieron dos publicaciones: la segunda edición elaborada entre 1834 y 1845; la tercera edición comienza después de la segunda guerra mundial comprendiendo los periodos entre 1951 y 1992.
A comienzos del siglo XIX, la palabra estadística adopta un significado más generalizado hacia la recolección y clasificación de cualquier tipo de datos cuantitativos.
William Playfair (1759-1823) expone su idea de que los gráficos permiten una comunicación más eficiente que las tablas de frecuencia. Es considerado como el inventor de los gráficos lineales, de barras y de sectores. Playfair publicó el libro titulado “The Commercial and Political Atlas” (1786) el cual contiene 43 gráficos de series de tiempo y por primera vez, es usado un gráfico de barras. En 1801 utiliza el primer gráfico de sectores en su obra “Playfair’s Statistical Breviary”.
Sir Francis Galton (1822-1911) creó el concepto estadístico de regresión y correlación, y fue el primero en aplicar métodos estadísticos para estudiar las diferencias humanas basadas en el uso de cuestionarios y entrevistas para recolectar los datos.
Herman Hollerith (1860-1929) fue un estadístico estadounidense quien desarrollo la primera máquina tabuladora basada en tarjetas perforadas y mecanismos eléctrico-mecánicos para el tratamiento rápido de millones de datos. Su máquina fue usada en el censo de 1890 en estados unidos que redujo la tabulación de los datos de 7 años (censo de 1880) a 2.5 años. Creó la firma “Computing Tabulating
Recording Corporation (CTR)”, que bajo la presidencia de Thomas J. Watson fue renombrada a “International Business Machines (IBM)” en 1924.
Major Greenwwod (1880-1949) investiga los problemas de salud asociados al trabajo en fábricas. Desarrolló la Epidemiología y en 1919 creó el Ministerio de la Salud en Inglaterra, responsable de datos estadísticos médicos.
DEFINICIÓN Y CLASIFICACIÓN
Como vimos en el apartado anterior, la estadística a variado su significado a través del tiempo, pasando de ser una herramienta usada solo para la administración de los gobiernos, a una ciencia con un sin fin de aplicaciones en diferentes disciplinas.
Estadística: La enciclopedia Británica define la estadística como la ciencia encargada de recolectar, analizar, presentar e interpretar datos.
La estadística pasa a ser una ciencia básica cuyo objetivo principal es el procesamiento y análisis de grandes volúmenes de datos, resumiéndolos en tablas, gráficos e indicadores (estadísticos), que permiten la fácil compresión de las características concernientes al fenómeno estudiado.
Estadística: El famoso diccionario Ingles Word Reference define la estadística como un área de la matemática aplicada orientada a la recolección e interpretación de datos cuantitativos y al uso de la teoría de la probabilidad para calcular los parámetros de una población.
Estadístico: Cualquier característica medible calculada sobre una muestra o población.
Los datos pueden provenir de una población o muestra. Esto datos deben ser cuantitativos, para así poder aplicar sobre ellos, operaciones aritméticas.
Muestra: Es un subconjunto de una población. Una muestra es representativa cuando los elementos son seleccionados de tal forma que pongan de manifiesto las características de una población. Su característica más importante es la representatividad.
La selección de los elementos que conforman una muestra pueden ser realizados de forma probabilística o aleatoria (al azar), o no probabilística.

Clasificación de la estadística
La estadística se puede clasificar en dos grandes ramas:
1. Estadística descriptiva o deductiva.
2. Estadística inferencial o inductiva.
La primera se emplea simplemente para resumir de forma numérica o gráfica un conjunto de datos. Se restringe a describir los datos que se analizan. Si aplicamos las herramientas ofrecidas por la estadística descriptiva a una muestra, solo nos limitaremos a describir los datos encontrados en dicha muestra, no se podrá generalizar la información hacia la población. La estadística inferencial permite realizar conclusiones o inferencias, basándose en los datos simplificados y analizados de una muestra hacia la población o universo. Por ejemplo, a partir de una muestra representativa tomada a los habitantes de una ciudad, se podrá inferir la votación de todos los ciudadanos que cumplan los requisitos con un error de aproximación.
LA INVESTIGACIÓN ESTADÍSTICA
El proceso de aplicación de la estadística implica una serie de pasos:

RECUERDA:
"EL CAMINO AL ÉXITO NO SIEMPRE ES LINEAL"
UN POCO DE HISTORIA
El uso de herramientas cuantitativas para el tratamiento de datos, tiene origen en épocas remotas. Se tiene información de hace más 3000 años antes de Cristo, donde las antiguas civilizaciones, como la Egipcia, aplicaron continuamente censos que ayudaban a la organización del estado y la construcción de las pirámides.
El antiguo testamento nos sugiere que Moisés ordenó un “Censo” a la población Israelita para identificar los miembros de las familias. En la antigua Grecia y el Imperio Romano, era común la aplicación de censos para la planificación de impuestos y la prestación del servicio militar.
La palabra estadística deriva del latín moderno statisticum collegium (“consejo de
estado”), del latín antiguo status (“posición”, “forma de gobierno”), de la palabra
italiana moderna statista (“estadista”, “político”) y del italiano antiguo stato (“estado”). En 1749, el alemán, Gottfried Achenwall (1719-1792) usa el término Statistik en su libro titulado “Staatswissenschaft der vornehmen Europäischen Reiche und Republiken”, quien originalmente designó la palabra estadística para el
análisis de los datos de un gobierno, definiéndola como la “Ciencia del Estado”. A
Gottfried Achenwall se le conoce como el “Padre de la Estadística”.
La primera persona que introdujo el término estadística en Inglaterra fue Sir John
Sinclair (1754-1835) con su trabajo “Statistical Account of Scotland” (1791-,1799) trabajo compilado en 21 volumenes. El autor explica en su libro, que la palabra estadística la adoptó gracias al estudio de investigaciones realizadas en Alemania, como una palabra novedosa que llamaría la atención de los ingleses; a diferencia, de que en Alemania la estadística se usa como instrumento para medir la fortaleza de un estado, mientras que Sinclair, la emplearía como generadora de información interna para encontrar falencias y proponer mejoras en el país. A este trabajo le siguieron dos publicaciones: la segunda edición elaborada entre 1834 y 1845; la tercera edición comienza después de la segunda guerra mundial comprendiendo los periodos entre 1951 y 1992.
A comienzos del siglo XIX, la palabra estadística adopta un significado más generalizado hacia la recolección y clasificación de cualquier tipo de datos cuantitativos.
William Playfair (1759-1823) expone su idea de que los gráficos permiten una comunicación más eficiente que las tablas de frecuencia. Es considerado como el inventor de los gráficos lineales, de barras y de sectores. Playfair publicó el libro titulado “The Commercial and Political Atlas” (1786) el cual contiene 43 gráficos de series de tiempo y por primera vez, es usado un gráfico de barras. En 1801 utiliza el primer gráfico de sectores en su obra “Playfair’s Statistical Breviary”.
Sir Francis Galton (1822-1911) creó el concepto estadístico de regresión y correlación, y fue el primero en aplicar métodos estadísticos para estudiar las diferencias humanas basadas en el uso de cuestionarios y entrevistas para recolectar los datos.
Herman Hollerith (1860-1929) fue un estadístico estadounidense quien desarrollo la primera máquina tabuladora basada en tarjetas perforadas y mecanismos eléctrico-mecánicos para el tratamiento rápido de millones de datos. Su máquina fue usada en el censo de 1890 en estados unidos que redujo la tabulación de los datos de 7 años (censo de 1880) a 2.5 años. Creó la firma “Computing Tabulating
Recording Corporation (CTR)”, que bajo la presidencia de Thomas J. Watson fue renombrada a “International Business Machines (IBM)” en 1924.
Major Greenwwod (1880-1949) investiga los problemas de salud asociados al trabajo en fábricas. Desarrolló la Epidemiología y en 1919 creó el Ministerio de la Salud en Inglaterra, responsable de datos estadísticos médicos.
DEFINICIÓN Y CLASIFICACIÓN
Como vimos en el apartado anterior, la estadística a variado su significado a través del tiempo, pasando de ser una herramienta usada solo para la administración de los gobiernos, a una ciencia con un sin fin de aplicaciones en diferentes disciplinas.
Estadística: La enciclopedia Británica define la estadística como la ciencia encargada de recolectar, analizar, presentar e interpretar datos.
La estadística pasa a ser una ciencia básica cuyo objetivo principal es el procesamiento y análisis de grandes volúmenes de datos, resumiéndolos en tablas, gráficos e indicadores (estadísticos), que permiten la fácil compresión de las características concernientes al fenómeno estudiado.
Estadística: El famoso diccionario Ingles Word Reference define la estadística como un área de la matemática aplicada orientada a la recolección e interpretación de datos cuantitativos y al uso de la teoría de la probabilidad para calcular los parámetros de una población.
Estadístico: Cualquier característica medible calculada sobre una muestra o población.
Los datos pueden provenir de una población o muestra. Esto datos deben ser cuantitativos, para así poder aplicar sobre ellos, operaciones aritméticas.
Muestra: Es un subconjunto de una población. Una muestra es representativa cuando los elementos son seleccionados de tal forma que pongan de manifiesto las características de una población. Su característica más importante es la representatividad.
La selección de los elementos que conforman una muestra pueden ser realizados de forma probabilística o aleatoria (al azar), o no probabilística.

Clasificación de la estadística
La estadística se puede clasificar en dos grandes ramas:
1. Estadística descriptiva o deductiva.
2. Estadística inferencial o inductiva.
La primera se emplea simplemente para resumir de forma numérica o gráfica un conjunto de datos. Se restringe a describir los datos que se analizan. Si aplicamos las herramientas ofrecidas por la estadística descriptiva a una muestra, solo nos limitaremos a describir los datos encontrados en dicha muestra, no se podrá generalizar la información hacia la población. La estadística inferencial permite realizar conclusiones o inferencias, basándose en los datos simplificados y analizados de una muestra hacia la población o universo. Por ejemplo, a partir de una muestra representativa tomada a los habitantes de una ciudad, se podrá inferir la votación de todos los ciudadanos que cumplan los requisitos con un error de aproximación.
LA INVESTIGACIÓN ESTADÍSTICA
El proceso de aplicación de la estadística implica una serie de pasos:

RECUERDA:
"EL CAMINO AL ÉXITO NO SIEMPRE ES LINEAL"
viernes, 27 de noviembre de 2009
Taller de refuerzo Tercer Periodo Matemáticas Grado 4°
Los siguientes ejercicios deberás presentarlos en un trabajo escrito como requisito para presentar el examen:
1. Dadas las fracciones:
A=3/4 B=2/5 C=1/2 D=2/3 E=1/4 F=3/10 G=7/8
A) Representa cada una de ellas.
B) Calcular los resultados de las siguientes operaciones y simplificar los resultados:
a. A + B
b. C – D
c. DxF
e. G ÷ B
f. D + C
g. (B +A) – E
h. (FxD) x B
i. A + B +D + C
j. E ÷ D
k. B ÷ A
l. (B ÷ A) + F
m. (D + C) x E
n. C ÷ G
o. A ÷ F + D
2. Dadas las siguientes fracciones, completar los espacios para que éstas sean equivalentes:
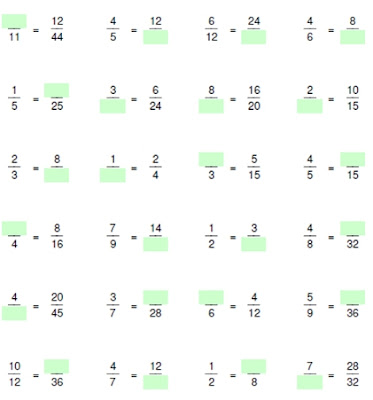
3. PROBLEMAS DE FRACCIONES 1
Problema 1:
Andrea compró una docena de huevos en un almacén. Al llegar a su casa se cayó y sólo
quedaron 5 huevos enteros. ¿Qué fracción de los huevos no se quebró?
Problema 2:
Un ciclista da diariamente 30 vueltas a una pista. Ayer, mientras hacía su rutina, comenzó una gran lluvia y sólo alcanzó a pedalear 13 vueltas. ¿Qué fracción de lo que normalmente recorre alcanzó a hacer?
Problema 3:
Una micro realiza el mismo recorrido 7 veces al día. Debido a la congestión vehicular hoy sólo recorrió 5 veces su ruta. ¿Qué fracción de su recorrido habitual logró hacer?
Problema 4:
En una competencia Juan ganó 15 bolitas. Si regaló 3 de ellas a su hermano menor, ¿qué fracción de las bolitas que había regalado ganó?
Problema 5:
En un almacén tenían 100 agendas para vender. Si vendieron sólo 78 agendas, ¿qué fracción del total vendieron?
Problema 6:
Francisca tomó una bebida de medio litro y María tomó dos bebidas de una cuarto de litro cada una. ¿Tomaron ambas la misma cantidad de líquido?
Problema 7:
Dos ciclistas deben recorrer un circuito. Si el primero ha recorrido dos tercios de éste y el segundo cuatro sextos del mismo, ¿han recorrido hasta ahora la misma distancia?
Problema 8:
En la especialidad de alimentación se preparan tortas para una recepción, Susana preparó 2 tortas de igual tamaño, una de piña y otra de manjar. La de piña la dividió en 24 trozos iguales y la otra en 12 trozos iguales. y don Juan comió 3 pedazos de torta de piña y dos de manjar, ¿comió lo mismo de ambas?
4. PROBLEMAS DE FRACCIONES 2
a. Luisa ha estudiado 12/5 horas, Pablo 5/6 horas menos que Luisa y Andrés tanto como Luisa y Pablo juntos. ¿Cuánto tiempo estudió cada uno?
b. Tenía $175.800. Gasté 4/5 de ese dinero en un obsequio para mi mejor amigo y ahorré el resto. ¿Cuánto dinero gasté? ¿Qué parte del dinero ahorré? ¿Cuánto dinero ahorré?
c. Luisa tenía $420.000. Gastó 1/3 de ese dinero en el centro comercial y 1/5 del resto en la pizzería. ¿Cuánto dinero gastó en el centro comercial? ¿Cuánto dinero gastó en la pizzería? ¿Cuánto le queda aún?
d. Un terreno de 180 kilómetros cuadrados se quiere repartir en lotes de 3/4 de kilómetro cuadrado. ¿Para cuántos lotes alcanza?
e. En una casa hay una llave atascada que gotea 1/10 de litro cada minuto. ¿Cuántos litros de agua se perderán en una hora?
f. En una competencia ciclística se recorren 1/2 km en la primera etapa, 4/5 km en la segunda etapa y 2/3 km en la tercera etapa. ¿Cuántos km en total se recorrieron en la competencia?
1. Dadas las fracciones:
A=3/4 B=2/5 C=1/2 D=2/3 E=1/4 F=3/10 G=7/8
A) Representa cada una de ellas.
B) Calcular los resultados de las siguientes operaciones y simplificar los resultados:
a. A + B
b. C – D
c. DxF
e. G ÷ B
f. D + C
g. (B +A) – E
h. (FxD) x B
i. A + B +D + C
j. E ÷ D
k. B ÷ A
l. (B ÷ A) + F
m. (D + C) x E
n. C ÷ G
o. A ÷ F + D
2. Dadas las siguientes fracciones, completar los espacios para que éstas sean equivalentes:

3. PROBLEMAS DE FRACCIONES 1
Problema 1:
Andrea compró una docena de huevos en un almacén. Al llegar a su casa se cayó y sólo
quedaron 5 huevos enteros. ¿Qué fracción de los huevos no se quebró?
Problema 2:
Un ciclista da diariamente 30 vueltas a una pista. Ayer, mientras hacía su rutina, comenzó una gran lluvia y sólo alcanzó a pedalear 13 vueltas. ¿Qué fracción de lo que normalmente recorre alcanzó a hacer?
Problema 3:
Una micro realiza el mismo recorrido 7 veces al día. Debido a la congestión vehicular hoy sólo recorrió 5 veces su ruta. ¿Qué fracción de su recorrido habitual logró hacer?
Problema 4:
En una competencia Juan ganó 15 bolitas. Si regaló 3 de ellas a su hermano menor, ¿qué fracción de las bolitas que había regalado ganó?
Problema 5:
En un almacén tenían 100 agendas para vender. Si vendieron sólo 78 agendas, ¿qué fracción del total vendieron?
Problema 6:
Francisca tomó una bebida de medio litro y María tomó dos bebidas de una cuarto de litro cada una. ¿Tomaron ambas la misma cantidad de líquido?
Problema 7:
Dos ciclistas deben recorrer un circuito. Si el primero ha recorrido dos tercios de éste y el segundo cuatro sextos del mismo, ¿han recorrido hasta ahora la misma distancia?
Problema 8:
En la especialidad de alimentación se preparan tortas para una recepción, Susana preparó 2 tortas de igual tamaño, una de piña y otra de manjar. La de piña la dividió en 24 trozos iguales y la otra en 12 trozos iguales. y don Juan comió 3 pedazos de torta de piña y dos de manjar, ¿comió lo mismo de ambas?
4. PROBLEMAS DE FRACCIONES 2
a. Luisa ha estudiado 12/5 horas, Pablo 5/6 horas menos que Luisa y Andrés tanto como Luisa y Pablo juntos. ¿Cuánto tiempo estudió cada uno?
b. Tenía $175.800. Gasté 4/5 de ese dinero en un obsequio para mi mejor amigo y ahorré el resto. ¿Cuánto dinero gasté? ¿Qué parte del dinero ahorré? ¿Cuánto dinero ahorré?
c. Luisa tenía $420.000. Gastó 1/3 de ese dinero en el centro comercial y 1/5 del resto en la pizzería. ¿Cuánto dinero gastó en el centro comercial? ¿Cuánto dinero gastó en la pizzería? ¿Cuánto le queda aún?
d. Un terreno de 180 kilómetros cuadrados se quiere repartir en lotes de 3/4 de kilómetro cuadrado. ¿Para cuántos lotes alcanza?
e. En una casa hay una llave atascada que gotea 1/10 de litro cada minuto. ¿Cuántos litros de agua se perderán en una hora?
f. En una competencia ciclística se recorren 1/2 km en la primera etapa, 4/5 km en la segunda etapa y 2/3 km en la tercera etapa. ¿Cuántos km en total se recorrieron en la competencia?
Taller de refuerzo Cuarto Periodo Matemáticas Grado 4°
Los siguientes ejercicios deberás presentarlos en un trabajo escrito como requisito para presentar el examen:
1. Completar los espacios en blanco con el dato que se indica:
80% = _____ (Fracción)
60% = _____ (Número decimal)
15% = _____ (Fracción)
22% = _____ (Número decimal)
82% = _____ (Fracción)
3,5% = _____ (Número decimal)
2. Calcula:
La cuarta parte de 300.
La tercera parte de 1704.
Las dos terceras partes de 54.
El 75% de 200.
El 50% de 1734.
El 120% de 248.
El 20% de 45.
El 130% de 120.
3. Realizar un esquema para resolver las siguientes situaciones:
a. Para programar las clases del lunes, el coordinador académico las ordenó de diversas maneras para elegir la más conveniente para los estudiantes. Observa y completa la tabla:
1° clase Ciencias
2° clase Español
3° clase Inglés
b. Las materias opcionales que ofrece un colegio son: danzas, teatro, música, pintura, títeres y costura. Si puedes escoger entre tres de estas materias, ¿cómo puedes seleccionarlas? ¿Cuántas probabilidades tienes para combinarlas?
C. Con los números 3, 5, 6, 7 y 9, ¿cuántos productos distintos se pueden obtener multiplicando dos de ellos?
4. Dada la siguiente información, realizar un diagrama de barras para representarla:
Prenda favorita Frecuencia
Blusa / / / / / / / / / / / / / / / /
Camisa / / / / / / / / / / /
Camiseta / / / / / / / / / / / / / / / / / / / / /
Jean / / / / / / / / / / / / / / / / / / / / / / / / / / / / / /
Falda / / / / /
¿Cuál es la moda?
5. Dada la siguiente tabla de datos, realizar el diagrama de barras
Deportes XXXXXX
Español XXXX
Inglés XXX
Matemáticas X
Ciencias XXXXXX
Sociales XXX
¿Cuál es la moda?
6. Dada la siguiente tabla, realizar el diagrama de barras y calcular el promedio de latas recogidas durante la semana
Día Total de latas
Lunes 125
Martes 150
Miércoles 200
Jueves 175
Viernes 150
Sábado 125
Domingo 100
7. Se preguntó a un grupo de 12 personas el número favorito y las respuestas fueron las siguientes:
8 – 9 – 10 – 6 – 9 – 10 – 5 – 3 – 6 – 9 – 10 – 11
a. En el anterior conjunto, la media o el promedio es:
b. En el anterior conjunto, la mediana es:
c. En el anterior conjunto, la moda es:
8. Durante un año la temperatura mensual promedio en grados centígrados de un lugar a las 12 m es:
Enero 24
Febrero 20
Marzo 18
Abril 19
Mayo 17
Junio 19
Julio 23
Agosto 18
Septiembre 21
Octubre 18
Noviembre 20
Diciembre 23
a. La moda es:
b. La media (o promedio) es:
c. La mediana es:
1. Completar los espacios en blanco con el dato que se indica:
80% = _____ (Fracción)
60% = _____ (Número decimal)
15% = _____ (Fracción)
22% = _____ (Número decimal)
82% = _____ (Fracción)
3,5% = _____ (Número decimal)
2. Calcula:
La cuarta parte de 300.
La tercera parte de 1704.
Las dos terceras partes de 54.
El 75% de 200.
El 50% de 1734.
El 120% de 248.
El 20% de 45.
El 130% de 120.
3. Realizar un esquema para resolver las siguientes situaciones:
a. Para programar las clases del lunes, el coordinador académico las ordenó de diversas maneras para elegir la más conveniente para los estudiantes. Observa y completa la tabla:
1° clase Ciencias
2° clase Español
3° clase Inglés
b. Las materias opcionales que ofrece un colegio son: danzas, teatro, música, pintura, títeres y costura. Si puedes escoger entre tres de estas materias, ¿cómo puedes seleccionarlas? ¿Cuántas probabilidades tienes para combinarlas?
C. Con los números 3, 5, 6, 7 y 9, ¿cuántos productos distintos se pueden obtener multiplicando dos de ellos?
4. Dada la siguiente información, realizar un diagrama de barras para representarla:
Prenda favorita Frecuencia
Blusa / / / / / / / / / / / / / / / /
Camisa / / / / / / / / / / /
Camiseta / / / / / / / / / / / / / / / / / / / / /
Jean / / / / / / / / / / / / / / / / / / / / / / / / / / / / / /
Falda / / / / /
¿Cuál es la moda?
5. Dada la siguiente tabla de datos, realizar el diagrama de barras
Deportes XXXXXX
Español XXXX
Inglés XXX
Matemáticas X
Ciencias XXXXXX
Sociales XXX
¿Cuál es la moda?
6. Dada la siguiente tabla, realizar el diagrama de barras y calcular el promedio de latas recogidas durante la semana
Día Total de latas
Lunes 125
Martes 150
Miércoles 200
Jueves 175
Viernes 150
Sábado 125
Domingo 100
7. Se preguntó a un grupo de 12 personas el número favorito y las respuestas fueron las siguientes:
8 – 9 – 10 – 6 – 9 – 10 – 5 – 3 – 6 – 9 – 10 – 11
a. En el anterior conjunto, la media o el promedio es:
b. En el anterior conjunto, la mediana es:
c. En el anterior conjunto, la moda es:
8. Durante un año la temperatura mensual promedio en grados centígrados de un lugar a las 12 m es:
Enero 24
Febrero 20
Marzo 18
Abril 19
Mayo 17
Junio 19
Julio 23
Agosto 18
Septiembre 21
Octubre 18
Noviembre 20
Diciembre 23
a. La moda es:
b. La media (o promedio) es:
c. La mediana es:
Taller de refuerzo Primer Periodo Física Grado 5°
La siguiente consulta deberás presentarla en un trabajo escrito:
1. Consultar la biografía de Isaac Newton, incluyendo en ella los aportes más significativos realizados a la física.
2. Consultar las dos primeras leyes de Newton, incluyendo las magnitudes en que se mide cada variable, y dar tres ejemplos de cada una.
3. En los siguientes enunciados decidir si son falsos o verdaderos y justificar cada respuesta:
a. Si un auto se mueve a velocidad constante, entonces está acelerado.
b. Si a una caja de 5 kg se le aplica una fuerza de 80 N, la aceleración será la misma que la que sufre una caja de 8 kg empujada por una fuerza de 50 N.
c. Una bola de 10 kg que cae libremente, sufre mayor aceleración que otra bola de 1 kg que también cae libremente. (Para este ejercicio realizar la experiencia con dos objetos diferentes, uno más pesado que el otro, y observar cuál cae primero)
d. Si viajas en un auto que se mueve a razón de 80 km/h, sientes que tu cuerpo se va hacia delante cuando el auto empieza a frenar, es decir, experimentas una desaceleración.
4. Consultar sobre algún experimento sencillo que puedas realizar sobre la aplicación de estas leyes.
1. Consultar la biografía de Isaac Newton, incluyendo en ella los aportes más significativos realizados a la física.
2. Consultar las dos primeras leyes de Newton, incluyendo las magnitudes en que se mide cada variable, y dar tres ejemplos de cada una.
3. En los siguientes enunciados decidir si son falsos o verdaderos y justificar cada respuesta:
a. Si un auto se mueve a velocidad constante, entonces está acelerado.
b. Si a una caja de 5 kg se le aplica una fuerza de 80 N, la aceleración será la misma que la que sufre una caja de 8 kg empujada por una fuerza de 50 N.
c. Una bola de 10 kg que cae libremente, sufre mayor aceleración que otra bola de 1 kg que también cae libremente. (Para este ejercicio realizar la experiencia con dos objetos diferentes, uno más pesado que el otro, y observar cuál cae primero)
d. Si viajas en un auto que se mueve a razón de 80 km/h, sientes que tu cuerpo se va hacia delante cuando el auto empieza a frenar, es decir, experimentas una desaceleración.
4. Consultar sobre algún experimento sencillo que puedas realizar sobre la aplicación de estas leyes.
Taller de refuerzo Primer Periodo Geometría Grado 5°
Los siguientes ejercicios deberás presentarlos en un trabajo escrito como requisito para presentar el examen:
1. En la figura mostrada, R1 R2 Y R3 son rectas y a, b, c, d. e, f, g y h son ángulos. Determina la medida de los ochos ángulos.

2. Determinar la medida de los ángulos interiores del triángulo mostrado y verificar que su suma es de 180º:

3. En la figura mostrada, determinar la medida de los ángulos internos del triangulo y los seis ángulos alrededor del punto P. Verificar que la suma de las medidas de estos seis ángulos es de 360º.

4. Determina las medidas de todos los ángulos mostrados en la figura:

5. Medir los cuatro ángulos mostrados y verificar que pares de ángulos tienen la misma medida:

1. En la figura mostrada, R1 R2 Y R3 son rectas y a, b, c, d. e, f, g y h son ángulos. Determina la medida de los ochos ángulos.

2. Determinar la medida de los ángulos interiores del triángulo mostrado y verificar que su suma es de 180º:

3. En la figura mostrada, determinar la medida de los ángulos internos del triangulo y los seis ángulos alrededor del punto P. Verificar que la suma de las medidas de estos seis ángulos es de 360º.

4. Determina las medidas de todos los ángulos mostrados en la figura:

5. Medir los cuatro ángulos mostrados y verificar que pares de ángulos tienen la misma medida:

Taller de refuerzo Segundo Periodo Geometría Grado 5°
Los siguientes ejercicios deberás presentarlos en un trabajo escrito como requisito para presentar el examen:
1. Revisar los siguientes pasos para construir la mediatriz de un segmento AB, y con ellos construir utilizando regla y compás, tres pares de rectas perpendiculares entre sí.
Mediatriz de un segmento: Es la recta que pasa justo por el punto medio del segmento
Construcción de la mediatriz de un segmento (Pasos)
a. Nombra al segmento trazado AB
b. Con el compás haciendo centro en el punto A traza un arco menor a la distancia del segmento.
c. Ahora, con centro en B, traza otro arco con igual abertura que el arco anterior, de manera que estos dos se corten.
d. Une los puntos en donde se cortaron los dos arcos por medio de una línea. El punto por donde corta esta línea al segmento es el punto medio.
2. Traza tres rectas cualesquiera de forma que estas se corten dos a dos. Traza la mediatrices de los segmentos formados entre estas. ¿Se cortan en un punto común?
3. Traza cuatro rectas cualesquiera de forma que estas se corten dos a dos. Traza la mediatrices de los segmentos formados entre estas. ¿Se cortan en un punto común?
4. En las siguientes figuras, señalar pares de rectas que sean paralelas y pares de rectas que sean perpendiculares:


5. Dibujar tres rectas paralelas separadas una de la otra cada 4 cm con una inclinación de 35º.
6. Dibujar cuatro rectas paralelas separadas una de la otra cada 5 cm con una inclinación de 85º.
1. Revisar los siguientes pasos para construir la mediatriz de un segmento AB, y con ellos construir utilizando regla y compás, tres pares de rectas perpendiculares entre sí.
Mediatriz de un segmento: Es la recta que pasa justo por el punto medio del segmento
Construcción de la mediatriz de un segmento (Pasos)
a. Nombra al segmento trazado AB
b. Con el compás haciendo centro en el punto A traza un arco menor a la distancia del segmento.
c. Ahora, con centro en B, traza otro arco con igual abertura que el arco anterior, de manera que estos dos se corten.
d. Une los puntos en donde se cortaron los dos arcos por medio de una línea. El punto por donde corta esta línea al segmento es el punto medio.
2. Traza tres rectas cualesquiera de forma que estas se corten dos a dos. Traza la mediatrices de los segmentos formados entre estas. ¿Se cortan en un punto común?
3. Traza cuatro rectas cualesquiera de forma que estas se corten dos a dos. Traza la mediatrices de los segmentos formados entre estas. ¿Se cortan en un punto común?
4. En las siguientes figuras, señalar pares de rectas que sean paralelas y pares de rectas que sean perpendiculares:


5. Dibujar tres rectas paralelas separadas una de la otra cada 4 cm con una inclinación de 35º.
6. Dibujar cuatro rectas paralelas separadas una de la otra cada 5 cm con una inclinación de 85º.
Suscribirse a:
Entradas (Atom)